基于ANSYS的O形密封圈可靠性分析及软件开
来源:液压气动与密封 时间:2020-06-08发布人:奇夏小编辑
第一作者简介:刘朋(1980-),男,江苏铜山人,高级工程师,本科,主要研究液压缸结构设计、轻量化与可靠性技术,工作于徐州徐工液压件有限公司。基金项目:国家重点研发项目(2018YFB2000904)摘 要:考虑随机不确定性因素的影响,对某型号O形密封圈进行可靠性分析。通过ANSYS参数化语言APDL建立O形密封圈参数化模型,根据应力-强度干涉模型及密封圈的工作特点建立其可靠性模型。假设密封圈的几何参数、载荷及屈曲强度为服从正态分布的随机变量,运用ANSYS的概率设计系统PDS对密封圈进行可靠性计算。利用VB6.0将ANSYS的APDL代码进行了封装,编写了O形密封圈的可靠性分析软件。该项研究可为液压元件的可靠性计算与专用软件开发提供借鉴意义。关键词:O形密封圈;可靠性;灵敏度;软件开发
由于结构简单、成本低廉O形橡胶密封圈广泛用于内燃机车、汽车、拖拉机、工程机械、机床及各种液压气动元件等密封,可承担固定、往复和旋转运动的密封,在机械产品的密封中O形橡胶密封圈占50%以上,O形密封圈的失效将严重影响整机的工作性能,因此,对O形密封圈的可靠性进行研究具有重要意义[1]。对O形密封圈研究一般是基于有限元分析或实验来进行的。桑勇、刘杰夫等都是基于ANSYS建立了O形密封圈有限元模型,分析了在不同压缩率、介质压力下O形密封圈最大Von Mises应力和最大接触压力的变化规律,为O形密封圈的结构设计及优化提供了理论基础和方法[2-3]。
对O形密封圈的可靠性分析,是在现有产品收集的各类数据及相关设计手册统计的各类资料(如材料性能分布等)基础上,运用相关分析理论预测所设计产品在规定使用工况下的可靠性,可靠性分析理论是基于概率的方法并以应力-强度干涉模型为基础的。
由基于概率的可靠性理论可知,液压缸在工作过程中受到各种因素的干扰,通常将结构本身的性质和外部作用效果定义为随机变量,主要分为两类:应力σ(外部作用效果)和强度δ(结构本身性质),结构可靠性设计的本质就是使结构所受最大应力(σmax)在一定概率程度上不大于其本身的强度δ,应力-强度模型恰好揭示了工程中结构可靠性分析的本质[4]。
基本变量和响应量之间的解析式一般很难确定,通过直接蒙特卡洛方法,即不断地对随机产生的一组输入变量进行计算,求出对应的响应量,不停地进行大量循环计算得到响应量的分布规律,一般情况下,循环次数越多,结果越准确。但对于复杂结构,由于计算时间长很难进行大量的循环计算,而用响应面法就很好地解决了这个问题[5]。响应面法假设随机输入变量对于随机输出变量的影响可以用数学函数来表达。因此,响应面法在随机输入变量空间中定位采样点,使得近似函数最有效,一般情况下,函数是一个二次多项式,那么拟合函数可以表示为:拟合出响应面之后,在响应面上进行蒙特卡洛抽样,此时不再需要对每一组输入进行有限元计算,循环计算的时间大大减少,因此对复杂结构进行足够多次的循环计算更加容易实现。
为研究材料、尺寸等不确定因素对产品性能及质量的影响,必须利用概率设计技术进行分析,将有限元分析技术与概率设计技术相结合,就是基于有限元的概率设计,即ANSYS提供的PDS技术(Probabilistic Design System)。对于概率设计问题而言,不确定性参数是采用某种概率密度函数来进行描述的,如几何尺寸或加工误差等服从高斯分布,且标准差在±3%~±5%之间,外部载荷也是服从一定分布的。在有限元分析过程中,输入参数几乎都存在一定的不确定性,将某些输入参数描述成服从某种分布的不确定性变量,经过大量的采样点计算统计分析出系统响应参数的分布特性、影响关系和影响程度等。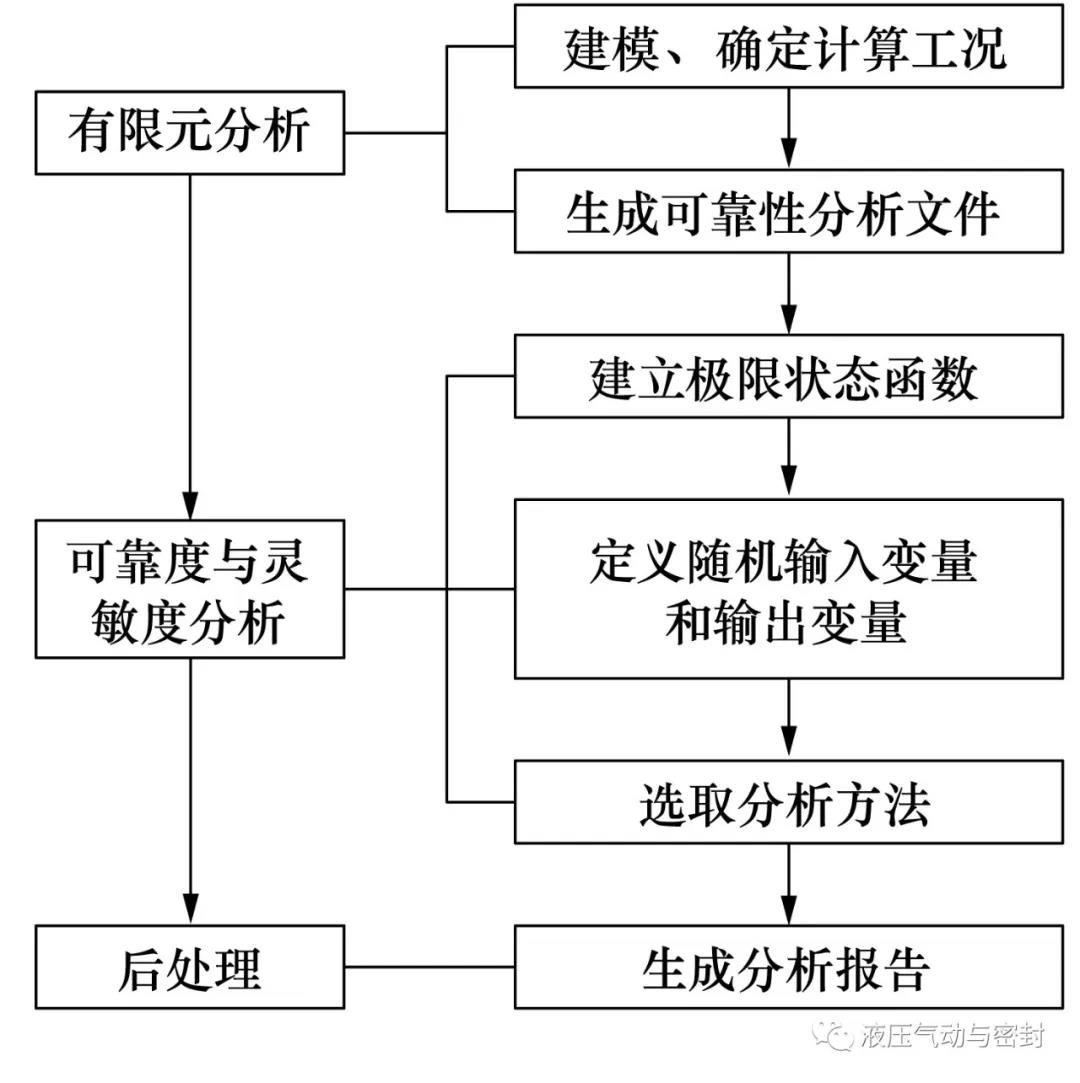
密封圈的材料假设为近似不可压缩的超弹性材料,其应力-应变表现为强烈的非线性,因此在有限元分析中采用能体现材料这一特点的两参数Mooney-Rivlin模型[6]来模拟O形密封圈材料,该模型的应变能函数如下式所示:
密封圈在工作过程中主要有三个接触面,包括缸体和密封圈之间的滑动接触面、密封圈和活塞凹槽之间的接触面、密封圈端面和凹槽端面之间的接触面。在接触分析时选择target169目标单元和contact172接触单元。在接触对中,将缸体和活塞凹槽作为目标面,将密封圈表面作为接触面。建立接触对时需要设置接触面之间的摩擦系数,通过查阅相关资料,取摩擦系数为0.3[8]。静密封O形圈在开始工作时可以认为经历两个历程:密封圈的安装和通入压力介质。密封圈的模型和加载如图2所示,通过两个载荷步可近似模拟密封圈的工作过程。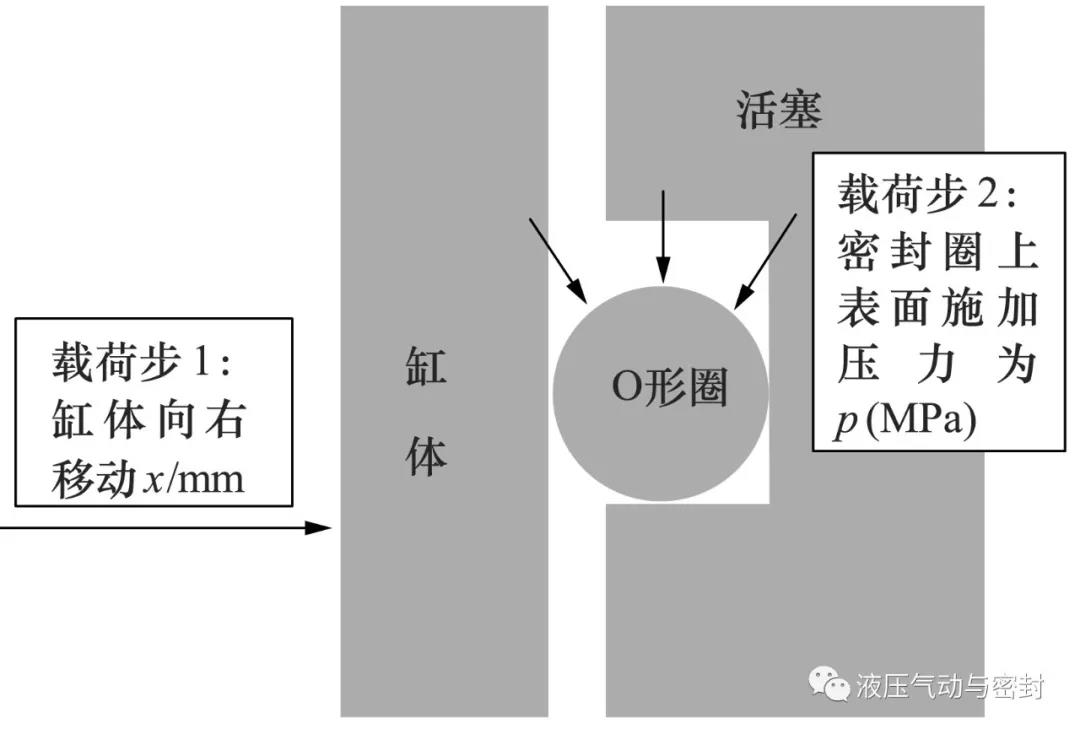
O形密封圈静力学分析结束后,在后处理中查看相应分析结果,其应力分析结果如图3所示。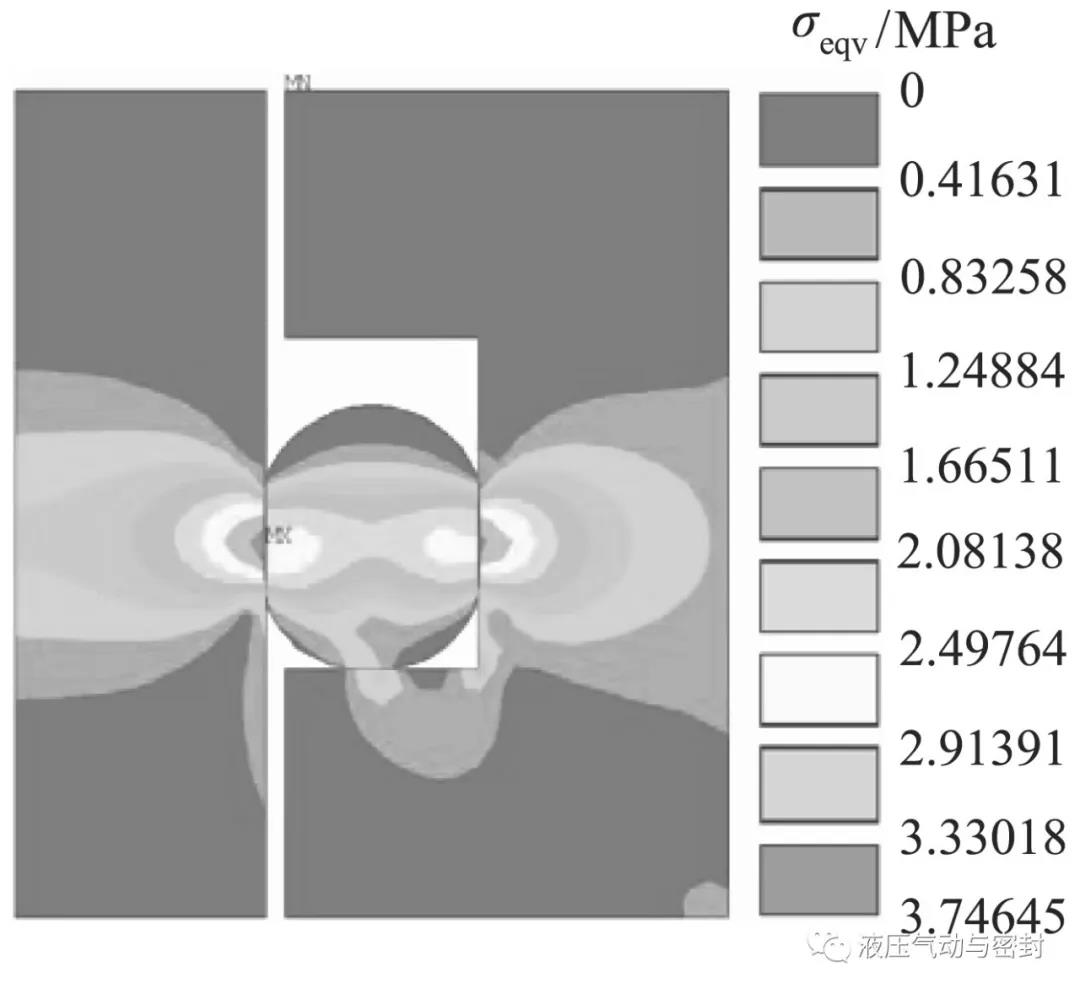
由图3可以看出,O形密封圈的最大应力发生在与缸体和活塞的接触部分,且最大应力为3.75 MPa,小于密封圈的强度,因此密封圈不会发生破坏。密封圈的应变云图和接触压力云图分别如图4和图5所示。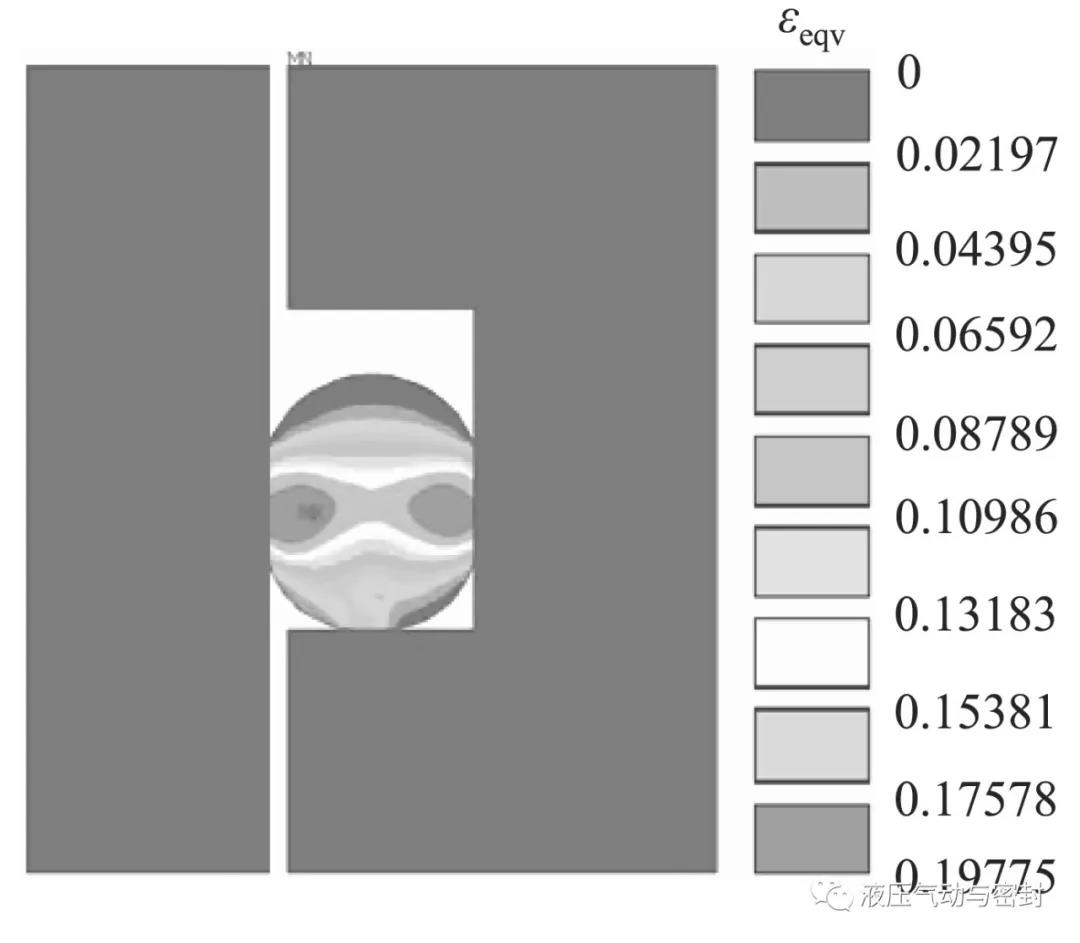
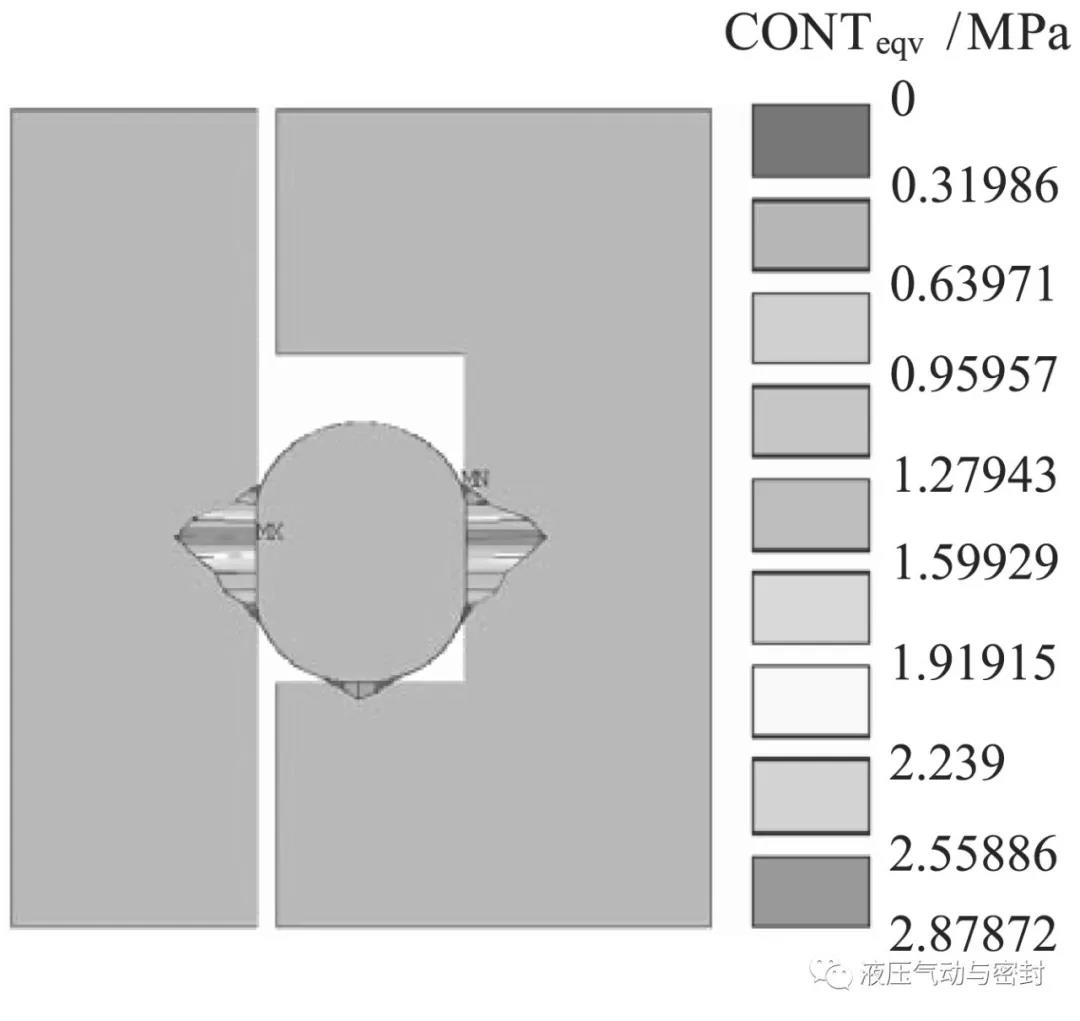
由图5可以看出,O形密封圈的最大接触压力发生在与缸体和活塞的接触部分,且最大接触压力为2.88 MPa,大于所施加的1 MPa的压力载荷,因此密封圈不会发生泄漏。2.4 生成可靠性分析文件
O形密封圈在工作过程中,其接触压力大于介质压力时可以保证不发生泄漏,其强度大于应力时可以保证密封圈不发生破坏。因此本文选择两种失效准则进行可靠性分析,分别是最大接触压力准则和强度准则。使用*GET命令分别提取应力和接触压力计算结果的最大值,并将其赋值给SMAX和pMAX,其命令流为:整理建立有限元模型、施加载荷、约束以及构建极限状态函数的程序代码,并通过LGWRITE命令生成概率分析文件,其命令流如下所示:2.5 设定输入输出
在对O形密封圈进行可靠性分析时,以密封圈的线径r、介质压力p、密封圈的强度S以及其弹性模量E为随机变量,具体的设置方法如以下命令流为:PDVAR,r,GAUS,2.65,0.1
PDVAR, p,GAUS,1,0.1
PDVAR,S,GAUS,10,1
输出变量为密封圈的极限状态函数ZS和ZP,其设置方法如以下命令流为:PDVAR,ZS,RESP
PDVAR,ZP,RESP
本文采用Box-Benhken矩阵抽样法来拟合响应面,经过13次循环后,得到了输出变量ZS和输入变量p、r之间的响应关系,可用图形显示输出变量与输入变量之间的响应关系,如图6所示。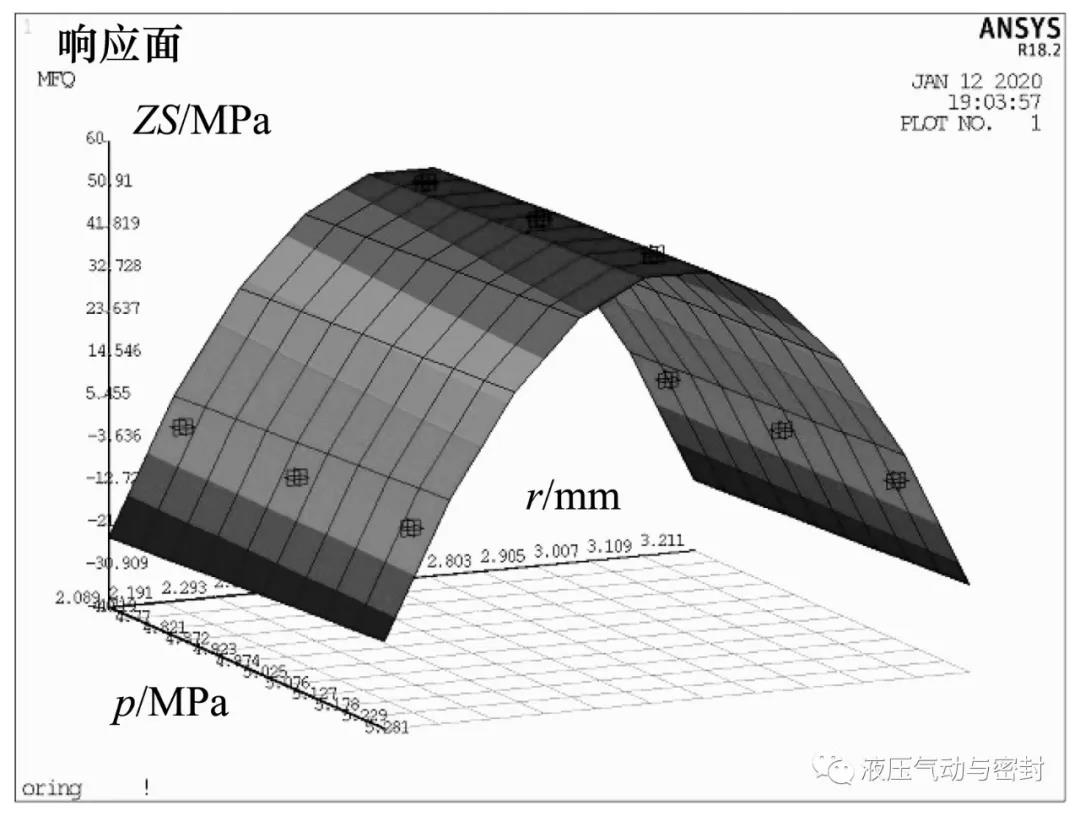
然后,在响应面上进行1000次蒙特卡洛循环计算,即对1000个输入变量不同的O形密封圈在不同工况下进行仿真分析,计算得到参数波动下的O形密封圈可靠度,输入变量r的历史抽样曲线如图7所示,该曲线显示了变量r的蒙特卡洛抽样历程。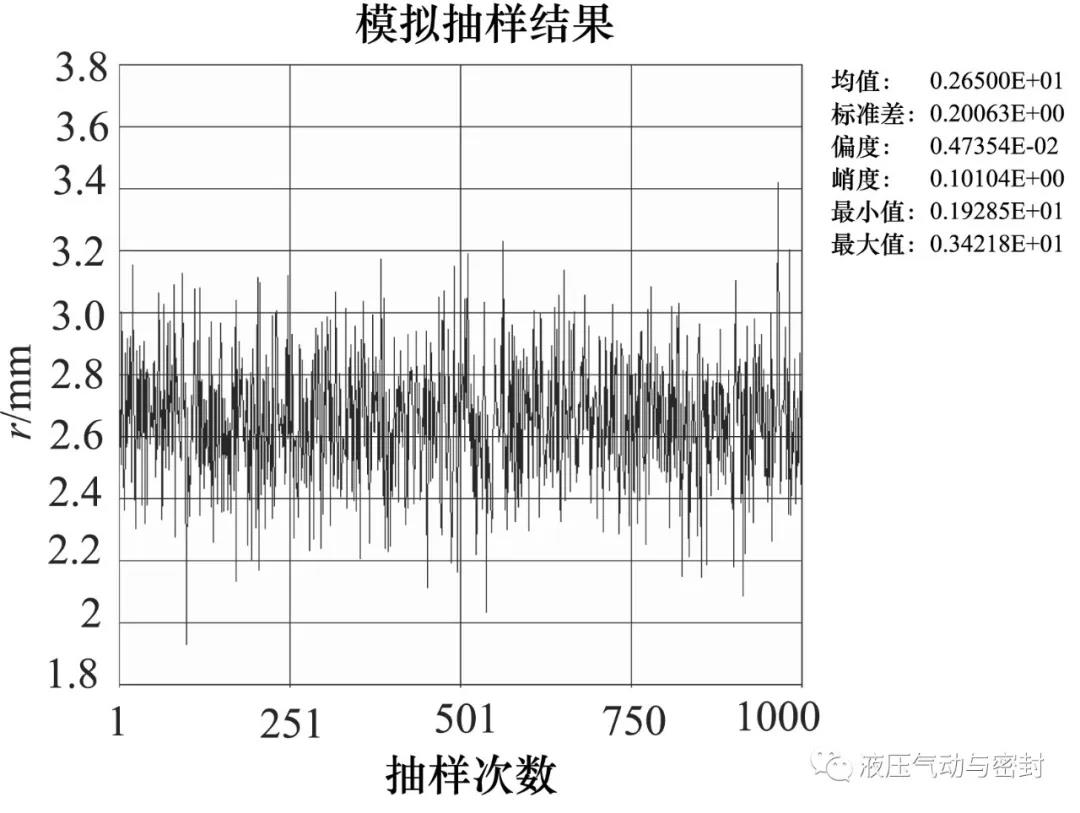
O形密封圈的极限状态函数ZS和PS的累积分布图分别如图8和图9所示。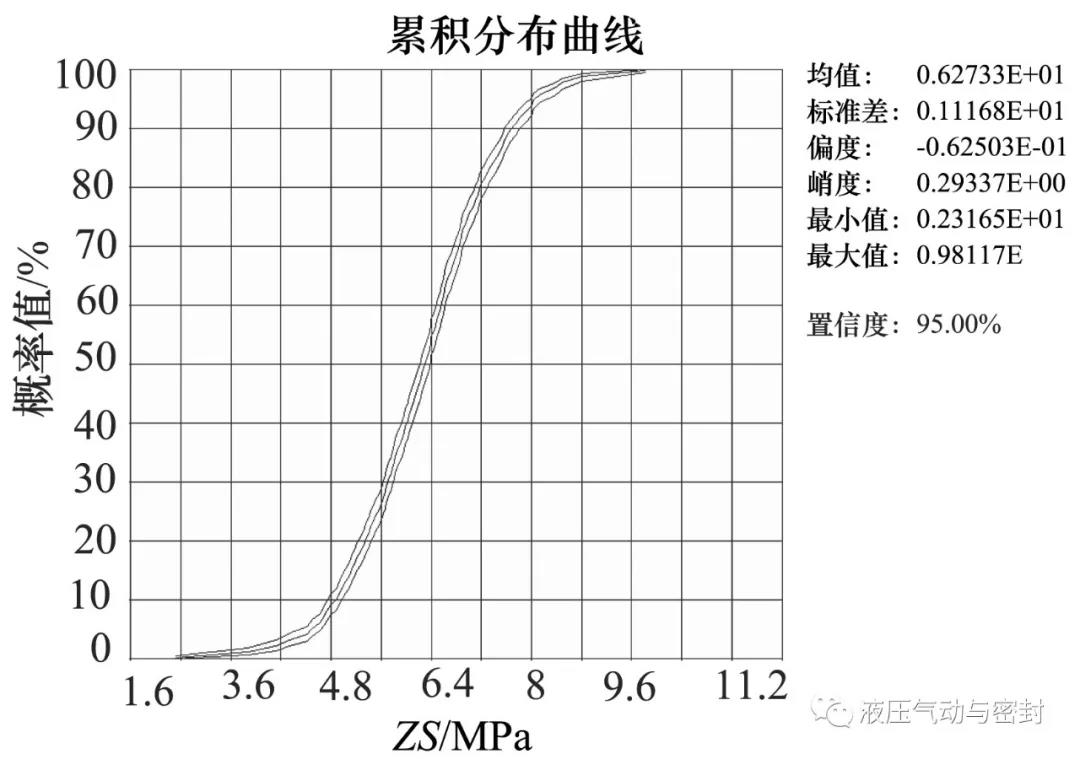
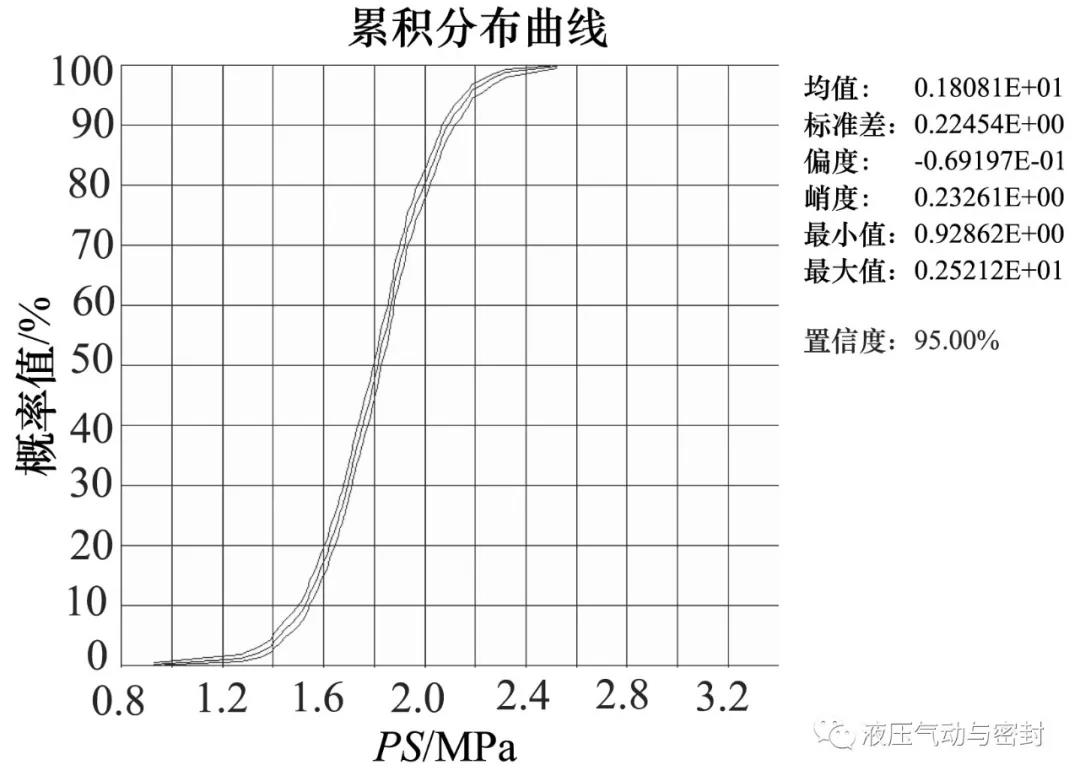
由图8和图9可以看出,O形密封圈的极限状态函数ZS和PS分别分布在1.8~9.6 MPa和0.8~2.6 MPa的范围内,而由前文的应力-强度干涉模型可知,极限状态函数只要分布在大于零的范围内结构即处于可靠状态,因此O形密封圈的可靠度为1,满足可靠度要求。
针对以上分析过程,利用VB6.0和ANSYS/APDL联合开发出一套O形密封圈可靠性分析软件,该软件可实现参数化建模、静力学分析、可靠性分析等功能,VB和ANSYS之间数据数据传递的流程如图10所示。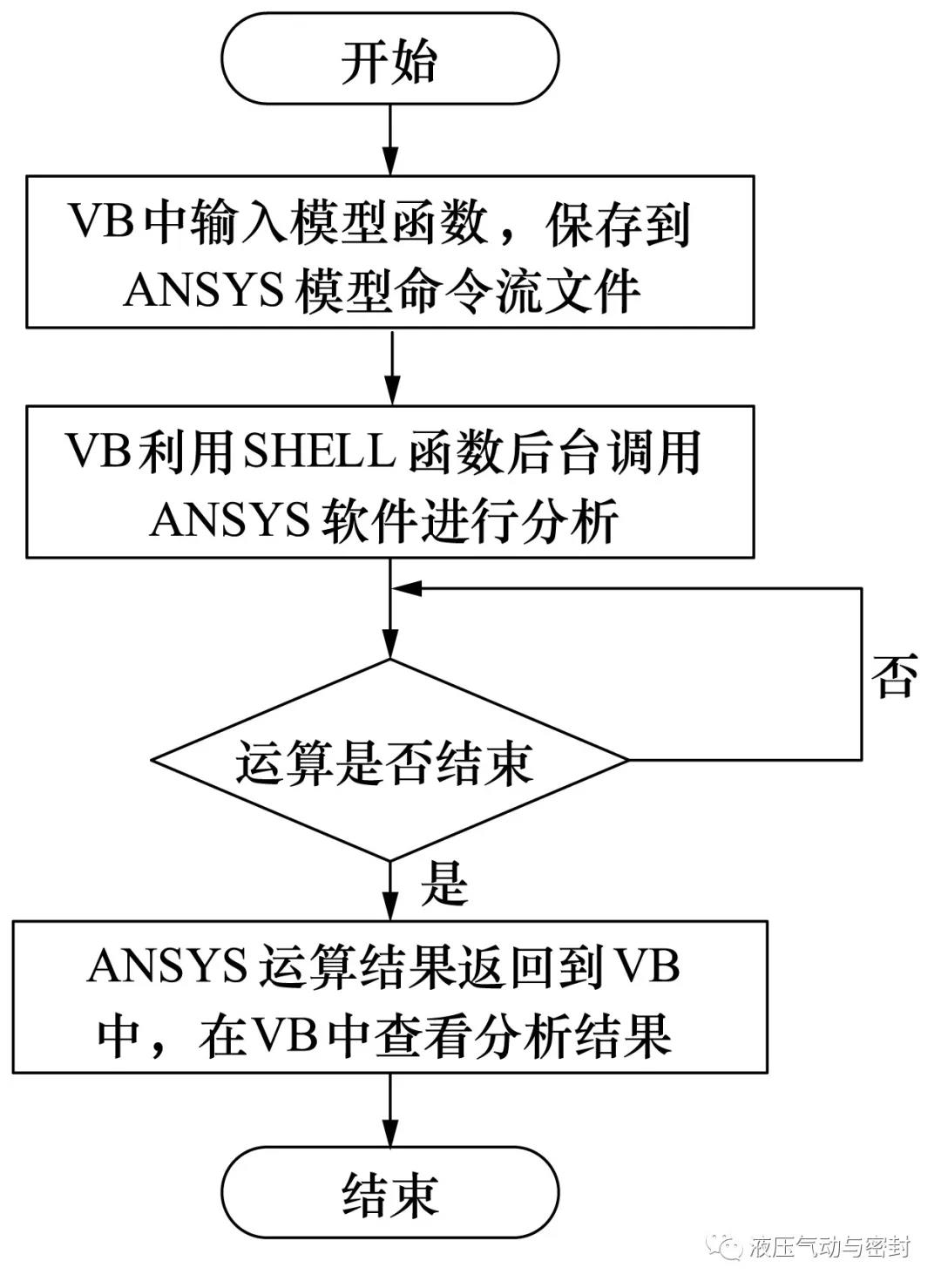
使用“SHELL”函数后台调用ANSYS执行密封圈应力分析文件“MFQYLFX.TEX”的语句如下所示:
该软件的登录界面如图11所示,输入用户名和密码,然后单击“登陆”按钮即可进入软件的主界面。
该软件的主界面如图12所示,菜单栏包括“系统”、“材料属性”、“模型参数”、“可靠性分析”和“帮助”菜单,其中“系统”菜单包含“选择ANSYS安装路径”、“修改密码”和“退出系统”子菜单,“可靠性分析”菜单包含“静力学分析”和“可靠度计算”子菜单。
模型的材料属性设置界面如图13所示,在该界面中可以设置缸体、活塞和O形密封圈的密度、弹性模量和泊松比。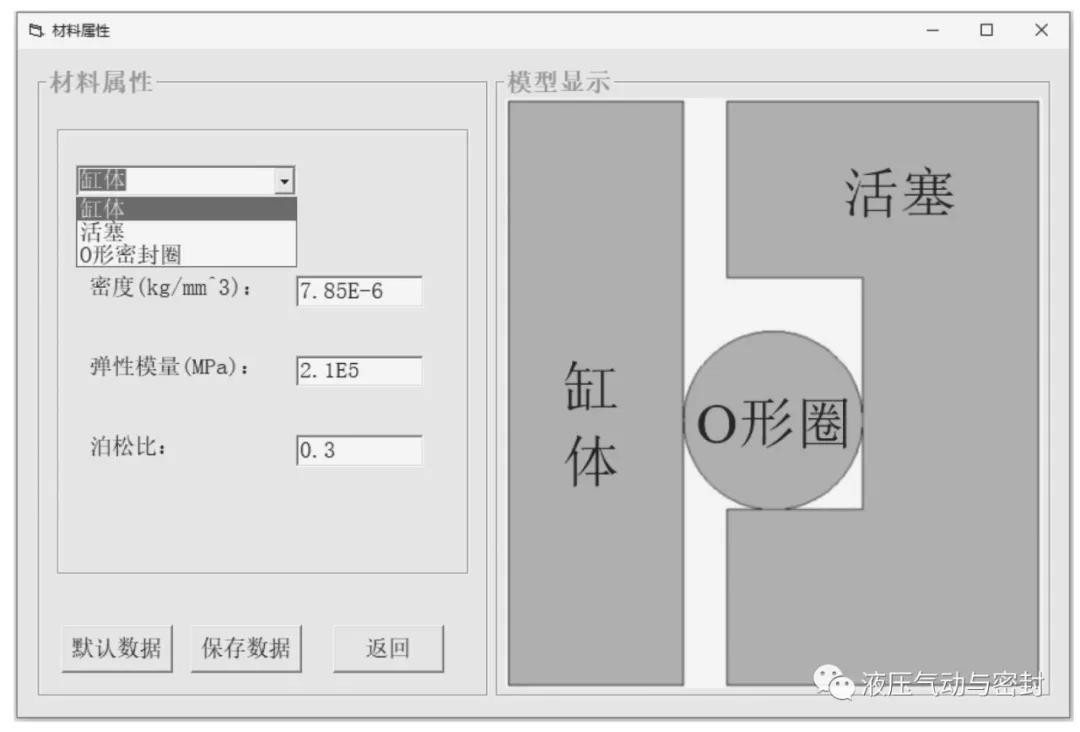
模型几何参数的设置界面如图14所示,在该界面中可以进行缸体、活塞和密封圈的几何参数设置。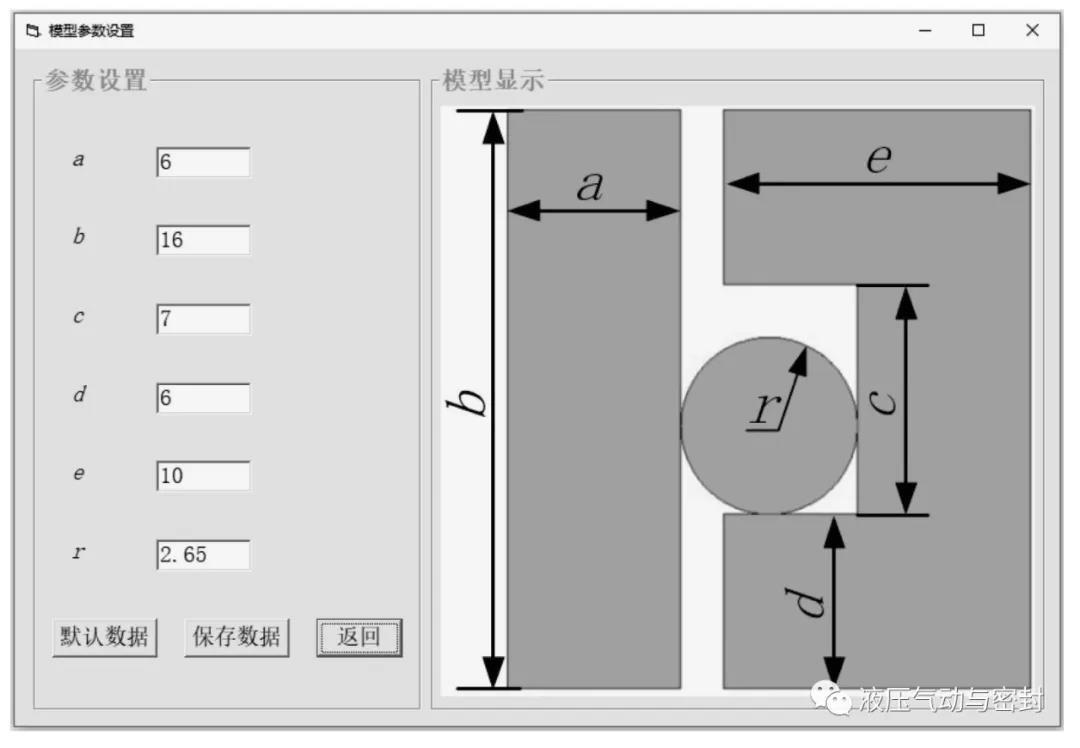
密封圈静力学分析结果如图15所示,该界面可以显示应力云图、应变云图、接触压力云图。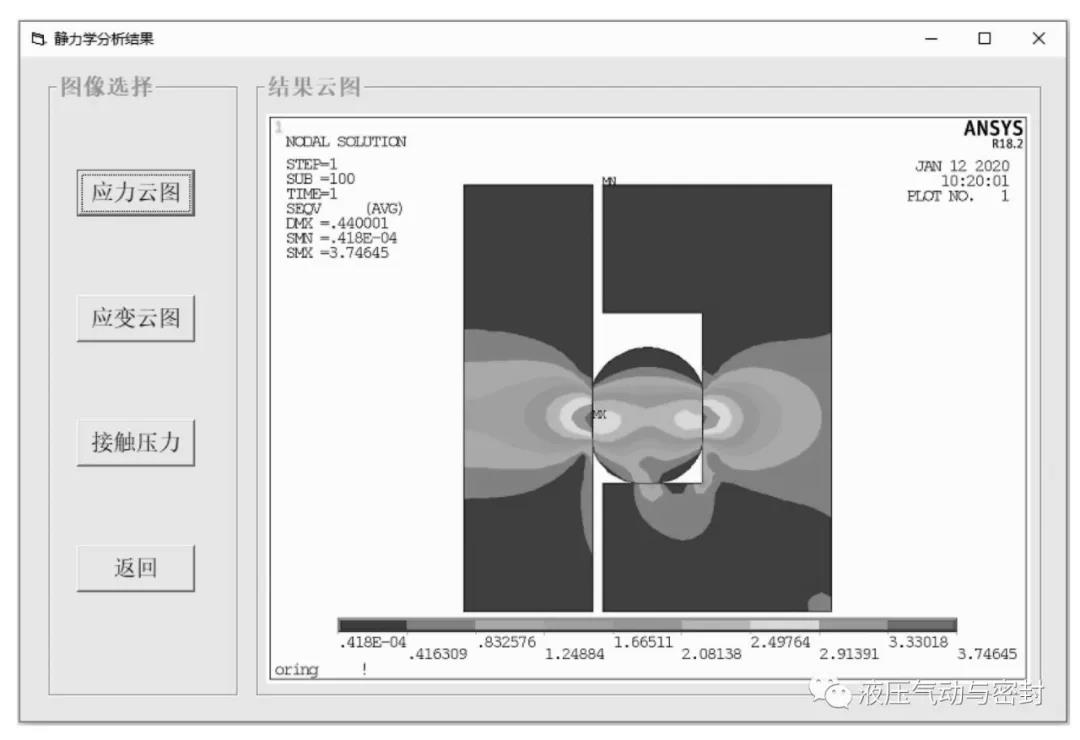
密封圈可靠性分析设置界面如图16所示,在该界面中可以进行输入变量、分布类型、可靠性分析方法、输出变量等的设置。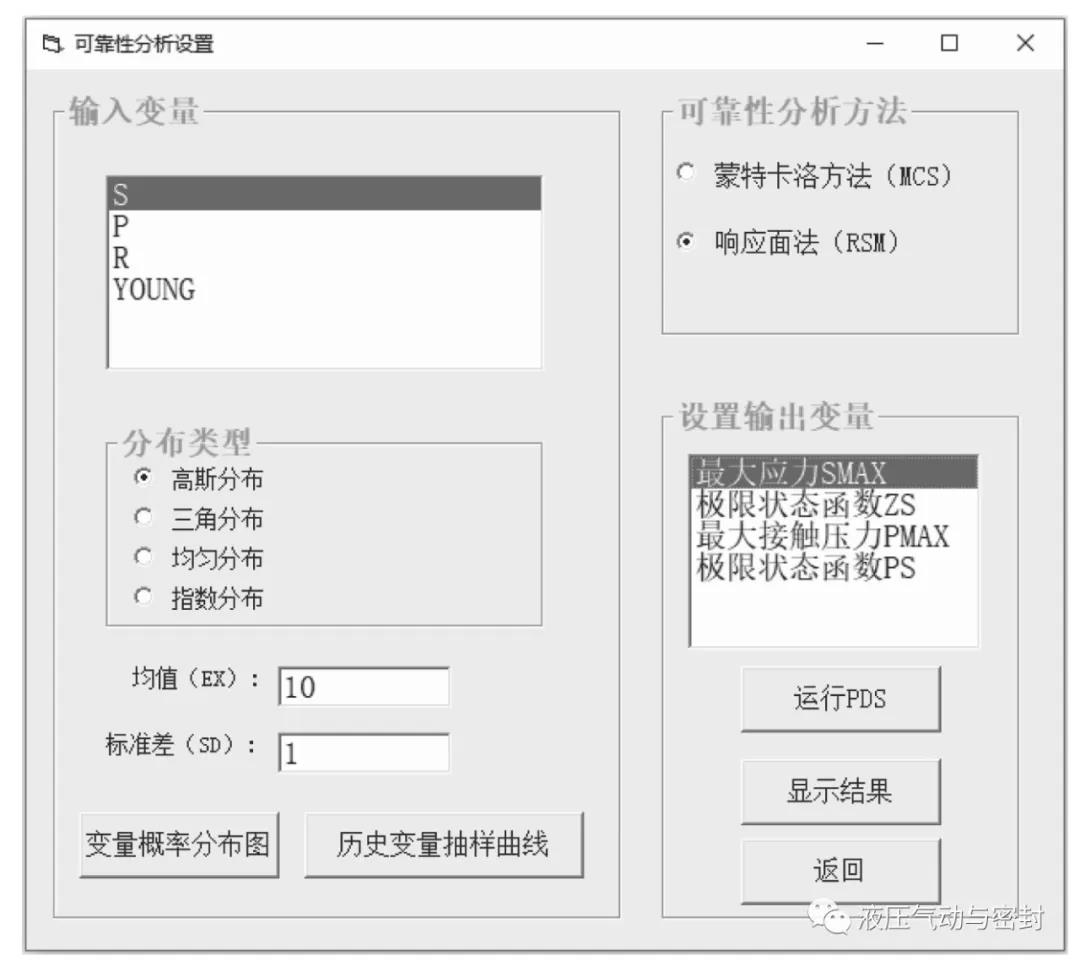
分析结束后,单击“变量概率分布图”和“历史变量抽样曲线”按钮可以得到如图17和图18所示的结果。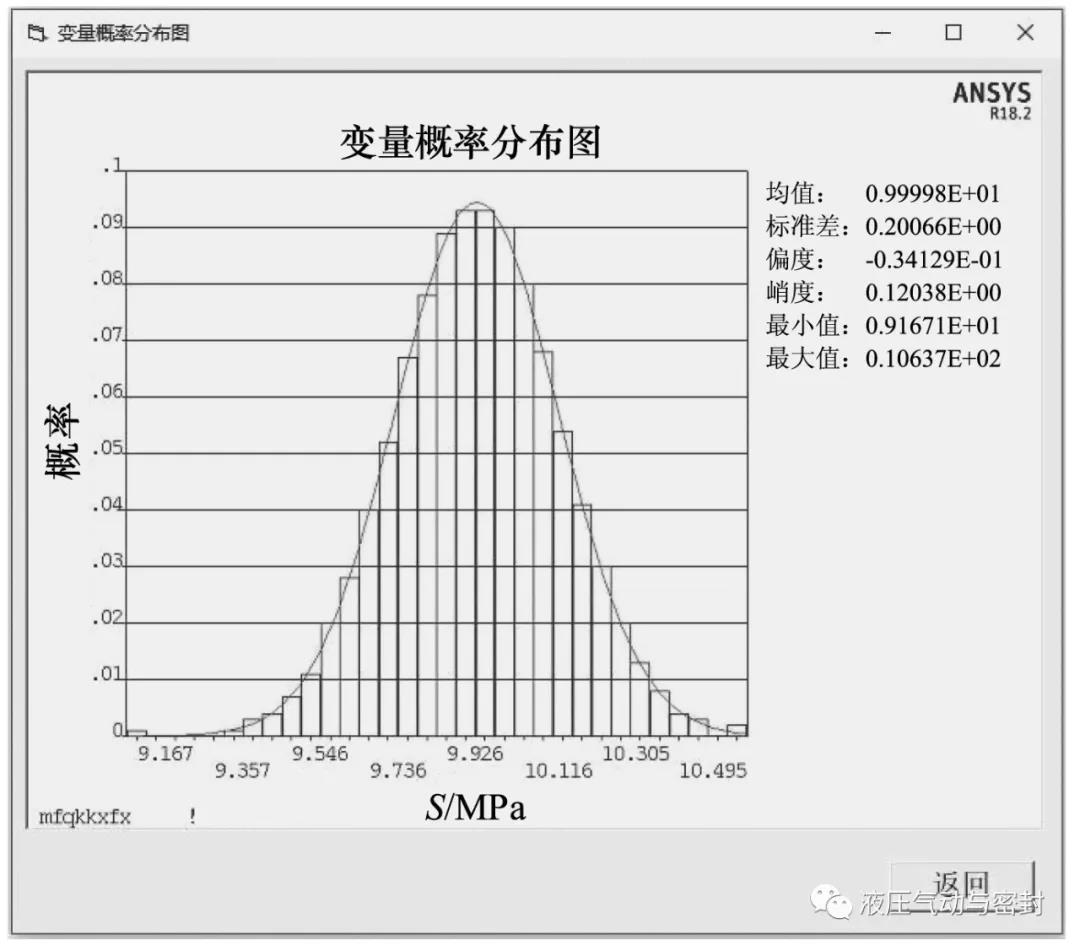
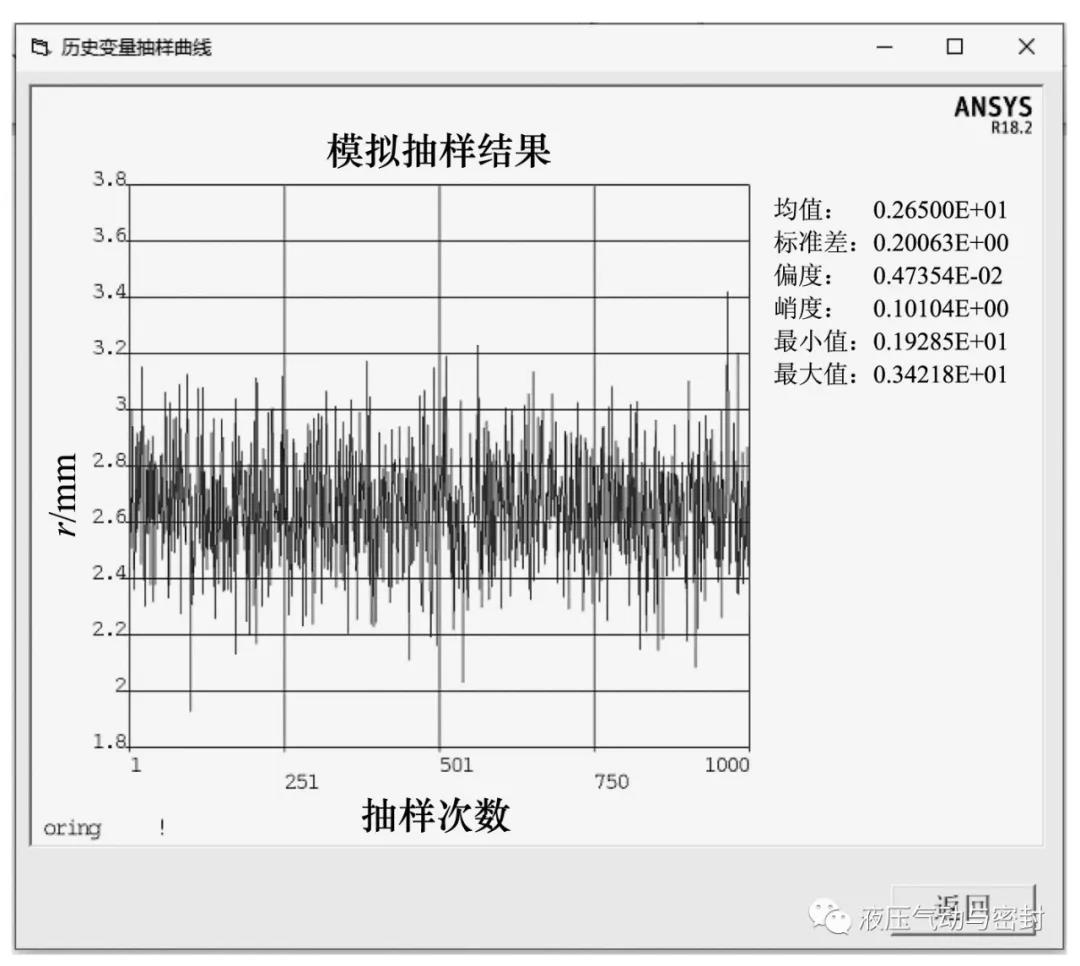
单击“显示结果”按钮可以得到如图19所示的“分析结果”界面,该界面可以显示响应面、累积分布图和灵敏度图。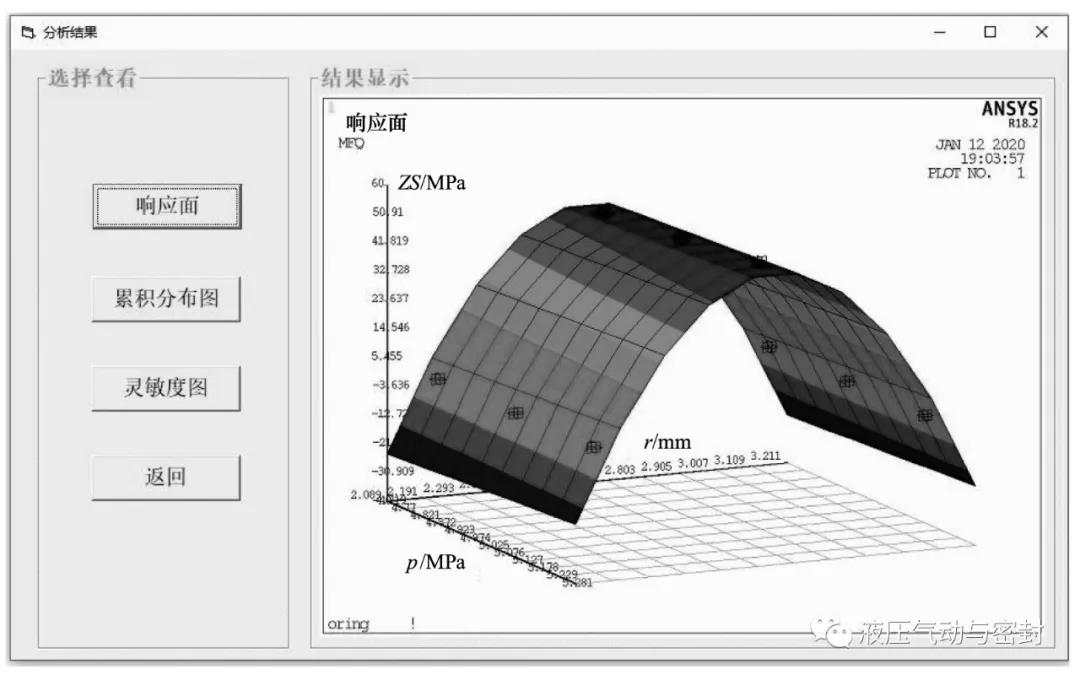
图19 结果查看
本文通过ANSYS/APDL建立了某型号O形密封圈的参数化模型,利用应力-强度干涉模型建立了极限状态函数,并结合ANSYS/PDS完成了O形密封圈的可靠性分析,结果表明其可靠度为1,满足可靠性要求,针对可靠性分析过程,利用VB6.0和ANSYS/APDL联合开发了O形密封圈可靠性分析软件,可以大大简化密封圈的可靠性分析工作,具有一定的工程意义。
本站刊载的某些内容(包括文字、图片、以及网页版面设计等)来源于网上引用或转载,仅为友情传播及阅读参考,不构成任何投资及应用建议。如涉及作者版权或其他问题,请尽快与本站联系,我们将在第一时间内配合处理或删除内容。转载请注明来源库优达。























